Check JEE Main Answer Key 2023, Solutions
The JEE Main Answer Key 2023 for the previous year is available in our article. There will be separate answer keys for all phases or sessions. JEE Main exam is organized by the NTA (National Testing Agency ). The JEE Main offers the candidate to take admission to various course programs like B.Tech, B.Arch, and B.Plan. The course programs are offered by the NITs, IITs, and IIITs, various Government and non-government engineering institutes, and universities. The following below are all the details regarding the JEE Main Answer Key 2023, Candidates can go through the article mentioned below.
JEE Main 2023 Answer Key
As soon as the examination over the JEE Main Answer key 2023 is released by the coaching institutes. The NTA will also release its answer key after a few days of examination. Candidates can check the answer key to evaluate their score and the right answer to the question. It also helps to whether he/ she will qualify or not so that they make their mind get ready to give the next phase exam and make their preparation too good for the next phase.
As it is announced by the authority that this year JEE Main 2023 Exam is in two-phase/ sessions so the jee main answer key for all two phases in January (24, 25, 28, 29, 30, 31 and 1st Feb) & April (06, 08, 10, 11, 12), will release after the end of each phase examination.
Latest Updates- 
How to Check JEE Main Official Answer Key 2023
The following steps that help the candidate check the JEE Main Answer key 2023 are given below.
- Firstly, Candidates are required to visit the official website.
- Now, they can enter their Application Number, Password, and Security pin.
- Then, click on the login button
- Now, the answer key for all sets will display on your computer screen.
- Then, download your required set answer key for JEE Main 2023.
- At last, candidates are requested to take the printout of the answer key so that they can evaluate their marks obtained.
Check JEE Main Session-1 Final Answer key 2023 Released. ![]()
Check JEE Main Session-2 Final Answer key 2022 Released.
Check JEE Main April Exam Official Final Answer key 2021 Released.
How to Challenge JEE Main Answer Key 2023
If candidates are not satisfied with the answer key released by the authority then they can challenge JEE Main 2023. Students can challenge the answers via an online process. For this candidate will have to fill out the application form and deposit Rs. 200/- per question. They can challenge the answers before the last date of the challenge. The challenges are accepted or submitted by post.
The application form fees for JEE Main answer Key 2023 can be submitted via online mode like a Credit card, Debit card, SBI Buddy, and Paytm. The application fee is non-refundable.
Jee Main Session-1- Answer Key Challenge 
JEE Main Answer Key by Coaching Institutes- 2023 
Session-1 Answer Key 2023
| Coachings | Date | Paper-1 ( B.E/ B.Tech ) | Subjects |
| Resonance | 24-Jan-2023 | Shift-1 | Physics, Chemistry, Mathematics |
| 25- Jan-2023 | Shift-1 | Chemistry, Mathematics | |
| Shift-2 | Physics, Chemistry, Mathematics | ||
| 29- Jan-2023 | Shift-1 | Mathematics | |
| Shift-2 | Physics, Chemistry, Mathematics | ||
| 30-Jan-2023 | Shift-1 | Physics, Chemistry, Mathematics | |
| Shift-2 | Chemistry, Mathematics | ||
| 31-Jan-2023 | Shift-1 | Chemistry, | |
| Shift-2 | Physics, Chemistry, Mathematics |
JEE Main Previous Year Answer key by Coaching Institutes
February Session- 2021
| Coachings | Date | Paper-1 ( B.E/ B.Tech ) | Subjects |
| Resonance | 24-Feb-2021 | Shift-1 | Physics, Chemistry, Mathematics |
| Shift-2 | Physics, Chemistry, Mathematics | ||
| 25-Feb-2021 | Shift-1 | Physics, Chemistry, Mathematics | |
| Shift-2 | Physics, Chemistry, Mathematics | ||
| 26-Feb-2021 | Shift-1 | Physics, Chemistry, Mathematics | |
| Shift-2 | Physics, Chemistry, Mathematics | ||
| Reliable Kota | 24-Feb-2021 | Shift-1 | Physics, Chemistry, Mathematics |
| Shift-2 | Physics, Chemistry, Mathematics | ||
| 25-Feb-2021 | Shift-1 | Physics, Chemistry, Mathematics | |
| Shift-2 | Physics, Chemistry, Mathematics | ||
| 26-Feb-2021 | Shift-1 | Physics, Chemistry, Mathematics | |
| Shift-2 | Physics, Chemistry, Mathematics |
March Session 2021
| Coachings | Date | Paper-1 ( B.E/ B.Tech ) | Subjects |
| Resonance | 16-March-2021 | Shift-1 | Physics, Chemistry, Mathematics |
| Shift-2 | Physics, Chemistry, Mathematics | ||
| 17-March-2021 | Shift-1 | Physics, Chemistry, Mathematics | |
| Shift-2 | Physics, Chemistry, Mathematics | ||
| 18-March-2021 | Shift-1 | Physics, Chemistry, Mathematics | |
| Shift-2 | Physics, Chemistry, Mathematics | ||
| Reliable Kota | 16-March-2021 | Shift-1 | Physics, Chemistry, Mathematics |
| Shift-2 | Physics, Chemistry, Mathematics | ||
| 17-March-2021 | Shift-1 | Physics, Chemistry, Mathematics | |
| Shift-2 | Physics, Chemistry, Mathematics | ||
| 18-March-2021 | Shift-1 | Physics, Chemistry, Mathematics | |
| Shift-2 | Physics, Chemistry, Mathematics |
April Session 2021 ( July Exam )
| Coachings | Date | Paper-1 ( B.E/ B.Tech ) | Subjects |
| Resonance | 20-July-2021 | Shift-1 | Physics, Chemistry, Mathematics |
| Shift-2 | Physics, Chemistry, Mathematics | ||
| 22-July-2021 | Shift-2 | Physics, Chemistry, Mathematics |
JEE Main 23rd Feb 2021/ Phase-1 Answer Key- Get Here
Shift-1
The shift-1 exam for Paper-2 ( B.Arch) candidates has been successfully done by the NTA. Talking about the overall paper was easy to moderate. The mathematics section is easy but the aptitude section is toughest than the previous year. Candidates were happy with the new exam pattern i.e optional questions in the Mathematics section. The following are the few questions with answers asked on day-1, the shift-1 paper of B.Arch is given below.
- Name the designers of the World Trade Center.
Minoru Yamasaki, Emery Roth - Find the equations of the normal to the curve x2 = 4y which passes through the point (1,2).
x+y = 3 - If x = cy + bz, y = az + cx, z = bx + ay, where x, y, z are not all zero, then a2 + b2 + c2 + 2ab = ?
1 - What is the minimum number of times a fair coin needs to be tossed, so that the probability of getting at least two heads is at least 0.96?
8 - If x >1, y > 1, z > 1 are in GP, then 1/(1 + lnx), 1/(1 + lny),1/(1 + lnz) are in?Answer, HP (Harmonic Progression)
- If A+B+C = 180 degrees. Then, find tanA + tanb + tanC =?
tanA tabB tanC - What are the number of divisors of the form (4n + 2), of the integer 240
20 - Find the area of the triangle formed by z, iz and z+iz.
1/2 |z|2 - The DE representing the family of curve Y2 (2c+x2021) where c is the positive parameter is of?
Order 1 - If z1 and z2 unimodular complex number that satisfy z12 + z22 = 4 then (z1 + z1)2 (z2 + z2)2 is equal to?
12 - The locus of the midpoint of the chord of the circle x²+y=4 which substance a right angle at the origin is?
x²+y²=2
Shift-2
Day-1, shift-2 Paper 2B ( B.Plan ) exam has been successfully done by NTA. Overall paper-2B is easy. The following are the few questions with answers asked in the exam is given below.
- What will be the area bounded by the curves y=rootx, 2y + 3 = x, and the x-axis in the 1st quadrant?
9 Square units. - If B and C are the square matrices of order n, and if A+B+C, BC=CB, C2 = 0. Then for any positive integer P, A^ P+1 = B^K * [B+(P+1) C]. What is K?
P - If a circle passes through the point (a, b) and cuts the circle x2 + y2 = k2 orthogonally, then what is the equation of the center?
2ax + 2by -(a2 +b2 + k2)=0 - The point on the curve y2 + 3x = 12y, when the tangent is vertical, is/are?
±4/√3, 2 - If f: (1, ∞) → (2, ∞) is given by f(n) = n + 1/n then f ^ -1 (n) equals?
n + (root(n2-4)) / 2 - If 0< P(A) < 1, 0< P(B) < 1 and P (A⋃B) = P (A) + P(B) – P(A) P(B), then select the appropriate answer.
P(A/B) = P(A) - If z1 and z2 are two non zero complex numbers such that |z1 + z2| = |z1| + |z2|, then arg z1 – arg z2 =?
0
JEE Main 24th Feb 2021/ Phase-1 Answer Key- Get Here
Shift-1
Paper-1 ( B.Tech ) has been successfully completed by the NTA. Following below some of the questions with answer asked in the JEE Main Paper-1, Shift-1.
- p, q > 0 and p + q = 2 and p4 + q4 = 272. Find the equation whose roots are p and q. x2 – 2x + 16 = 0
- Find the area of the region inside the circle x2 + y2 = 36 and outside the parabola y2 = 9x.
- If the tangent to the curve y = x3 at the point P (t, t3) meets the curve again at Q, then the co-ordinate of the point which divides PQ internally in the ratio 1:2
- From 6 Indians and 8 Americans, a committee is formed which includes at least 2 Indians and double the number of Americans as Indians. Find the number of ways is
1625 - f(x) = 4×3 – 3×2 / 2 – 2sinx + (2x-1) cosx:
Increases in [1/2, ∞] - If R —–> R is a function defined by (x) = [x – 1] cos (2x-1 / 2)⊼ where [.] —>gif
Continuous for every real x - If the imaginary part of expression z-1 / eiθ + eiθ / z-1 is zero, the locus of z is
- The tangent to the curve x = a (0 – sinθ), y = a(1+cosθ) at the point θ = (2k+1)x, k ∊ I are parallel to
y = 0 - Compare the Ionisation Energy of SC, RI, V, Cr, Mn…
- What is the composition of gunmetal?
88 percent copper, 10 percent tin, and 2 percent zinc - The solution of differential equation xdy – ydx = √x2 + y2 dx is
y + √x2 + y2 = cx2 - The equations of AM and EC are given, then find the percent of modulation.
- The ratio of effusion does not depend on _
Size of molecule - An ore of Tin containing FeCrO4 is concentrated by _
Magnetic separator - A cube is given and it has -q charge in one corner and +q charges in all the remaining 7 corners. Find the electric field inside the cube.
- The non-existence of PbI4 is due to __
Small size of Pb ion and large size of I ion. Highly reduced the power of I ion. - Block m has amplitude A. If another mass of m is added what will be the new amplitude?
- A body cools down from 100C to 90C in 20 minutes. It will cool down from 110C to 100C in _
Less than 20 minute - A P and V graph was given, find the work done.
- If there is a degradation of vegetation, then what effect is caused in the environment from gas released?
- An astronaut has left the international space station to test a new space scooter. His partner measures the fall velocity changes which take place in 10s interval. Find the magnitude and direction of average acceleration at the beginning of the 10-sec interval, the astronaut is moving towards the x-axis in 10m/sec, and at the end is 10 sec. He is moving towards the -ve axis at 5m/sec.
1.5 m/sex, -ve x-axis - What will be the energy if you increase lambda
- If a dice is rolled n times. If the probability of getting an even number and an odd number is equal then find n.
- Two capacitors are given. Find the series and parallel resistance and their ratio.
- Find the work done by the cylcin process.
- Calculate the ionization energy of all third-period elements.
Shift-2
Day-2, shift-2, Paper-1 ( B.E/ B.Tech ) question with answer is given below.
- Find the area enclosed by the parabolas y = 5×2 and y = 2×2 + 9.
- Given y = (x) such that x dy/dx + y = bx4 then find b
10 - Find the point on y = x2 + 4 which is at the shortest distance from the line y = 4x -4
2,8 - Question,
 Answer, Correct Option is [C]
Answer, Correct Option is [C] - Question,
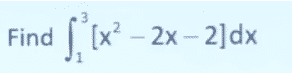
-1 -√2 -√3 - If A is symmetric matrix and B is a skew matrix of order 3×3, then consider (A2B2 – B2A2) X = 0, where X is a matrix of unknown variables of 3×1 and O is a null matrix of 3×1, then the system of linear equation is
∞ solution - Question,
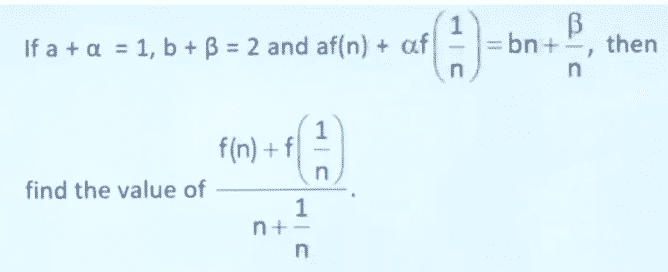
- Answer, 2
- The variance of 10 natural numbers 1, 1, 1, ….., k is less than 10. Find the maximum value of k.
6 - An airplane at point A gives an angle of elevation 60o and after 20 seconds when the airplane is moving with speed 432 km/hr and making an angle of 30o. Then find the height of the airplane in meters.
1200√3 - Evaluate tan (1/4 sin-1 )√63/8)
4-√7/3 - A rod of mass M of length L is bent in the form of a hexagon. Then MOI about an axis passing through geometric center & perpendicular to the plane of the body will be?
ML2/216 - The Broglie wavelength of proton & particle are equal to the ratio of their velocities is
1:4 - The weight of a person on a pole is 48 N then the weight on the equator is?
47.84 - Two electrons fixed at a separation of 2d from each other. A proton is placed at the midpoint and is displaced slightly in a direction perpendicular to the line joining two electrons. Find the frequency of oscillation of the proton.
- In Young’s double-slit experiment. What will happen if the red light is replaced by violet light?
λ↓ β ↓ - Maximum frequency in transition
n = 2 —->1 - produced of a photon?
-1nm - Two electrons were placed 2d distance apart, a proton was placed at the middle and shifted x<<d, the system performs shm , then the frequency of oscillation will be?
- A traveling wave represented by
- A particle O at x-axis and damping force F = x2 is constant acting on it before comes to rest. The distance traveled by particle.
(3mu2 / 2a)1/3 = x - Where will the center of mass of the disc shift when a cavity of radius R/2 is cut from it?
- 12NC charge over 6cm of a 12 cm x 12 cm square. What is the flux through the square?
22.59 x 104 T-m2 - Length 1m can be measured up to 0.01m, time period 1.955, 0.01-time accuracy. What is the erroring?
Around 2% - What happens in the domain of ferromagnetic material is placed in an external magnetic field.
May increase or decrease in size - Two carts are moving toward each other at a speed of 7.2kmph. Each blow horn 676 Hz. The velocity of air is 340> What is beat heard by each.
8 - Two masses 1 kg and 2kg moving with equal momentum. Find the ratio of K.E.
k1:k2 = 2:1 - Half the life of a reaction is 3.33 hrs. Sucrose —-> glucose + fructose after 9 hrs fraction of sucrose left is f. Then calculate the value of log (1/f).
0.9 - If a compound CxHy required 6 times the volume of O2 then itself and produced 4 times the volume of CO2 then find y.
8 - Question,
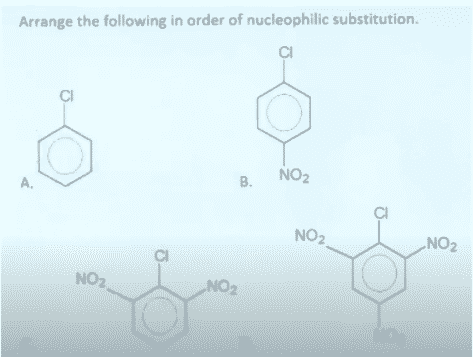
- Answer, D, C, B, A
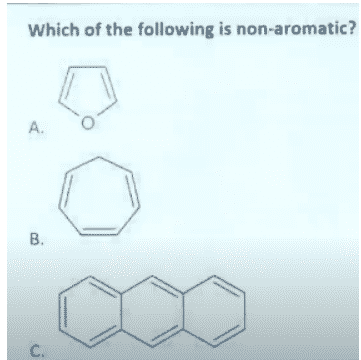
- Answer, Correct option is [B]
- Statement 1: Hydrogen is most abundant in the universe but not in the earth’s troposphere.
Statement 2: Hydrogen is the lightest element
Both statements are correct, and the second is the correct explanation for statement-1 - NO2 forms dimer but ClO2 does not. Why?
in ClO2, unshared electron present in sp3orbital - Question,
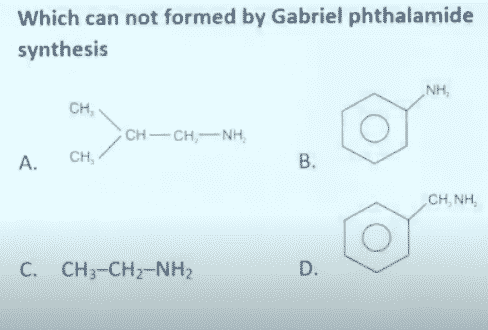
- Answer, Correct option is [B]
- What is the correct order of density for Zn, Fe, Co, Cu, Cr
Cu> Co> Fe> Cr> Zn - In Buna S, S is for
Styrene - p, q > 0 and p + q = 2 and p4 + q4 = 272. Find the equation whose roots are p and q.
x2 – 2x + 16 = 0 - Find the area of the region inside the circle x2 + y2 = 36 and outside the parabola y2 = 9x.
- If the tangent to the curve y = x3 at the point P (t, t3) meets the curve again at Q, then the co-ordinate of the point which divides PQ internally in the ratio of 1:2
- From 6 Indians and 8 Americans, a committee is formed which includes at least 2 Indians and double the number of Americans as Indians. Find the number of ways is
1625 - f(x) = 4×3 – 3×2 / 2 – 2sinx + (2x-1) cosx:
Increases in [1/2, ∞] - If R —–> R is a function defined by (x) = [x – 1] cos (2x-1 / 2)⊼ where [.] —>gif
Continuous for every real x - If the imaginary part of expression z-1 / eiθ + eiθ / z-1 is zero, the locus of z is
- The tangent to the curve x = a (0 – sinθ), y = a(1+cosθ) at the point θ = (2k+1)x, k ∊ I are parallel to
y = 0 - Compare the Ionisation Energy of SC, RI, V, Cr, Mn…
- What is the composition of gunmetal?
88 percent copper, 10 percent tin, and 2 percent zinc - The solution of differential equation xdy – ydx = √x2 + y2 dx is
y + √x2 + y2 = cx2
JEE Main Previous Year Answer Key
Candidates can also check the previous year’s answer key to know the previous year’s answers to the question. Candidates are also requested to solve the previous year’s questions asked in the exam and solve the modal paper. The previous year’s answer key is given below.
JEE Main 24th Feb 2021/ Phase-1 Answer Key- Get Here
Shift-1
- Question-1, Integral value of k for which x2 -2(3k-1) +8k2 -7 > 0
3 - Question-2, The number of points where f(x) = |2x+1| -3 |x+2| + |x2 + x -2|, n∊R is not differntiable is
3 - Question-3, Curve passing through (0,0) and slope of the tangent to it any point (x,y) is x2 – 4x + y +8/ x-2, then this curve also passes through
(5,5) - Question–4, For any two statement p and q ~ (p v q) v (~p ^ q), is logical to
~p - Question-5,
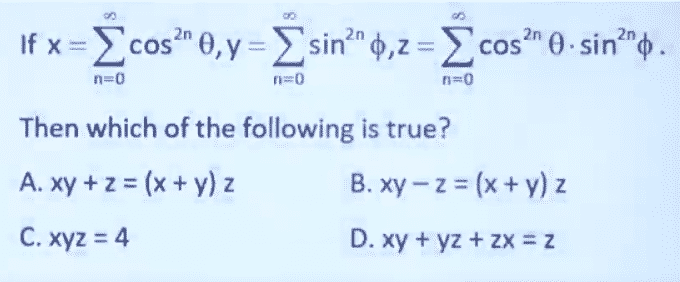
Correct option is [A] - Question-6,
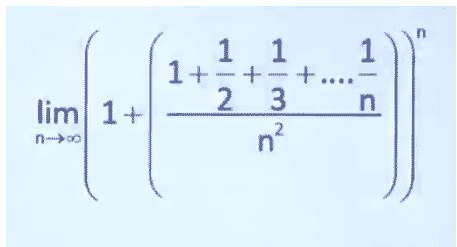
1 - Question-7, Out of 30 observations, 10 observations are (1/2, -d) and 10 observations are d and the remaining 10 are (1/2 + d). If the variance of 30 observation is 4/3, then d is
- Question-8, A man watches a boat traveling towards him while standing on a top. Its deviation is 30 degrees. After 20-sec deviation changes to 45 degrees. Then how much time it takes to reach the bottom of the tower?
20√3/√3-1 - Question-9, If straight line x+2y = 1 cuts axis at A and B and circle passes through points A, B, and origin. Then the sum of height the perpendicular drawn from A and B on a tangent at the origin of the given circle is
√5/2 - Question-10, Locus of the center of a circle which touches x2 + y2 – 6x – 6y + 14 + 0 externally and also touches the y-axis.
y2 – 6y – 10x + 14 = 0 - Question-11, Find the total number lying between 100 and 1000 formed using 1,2, 3, 4, 5 and divisible by either 3 or 5.
415 - Question-12, Graph of log K and 1/T was given for which slope = -10000K if T is 500 Kelvin and rate constant is 10-5 at which temperature value of the rate constant will be 10-4
565 Kelvin - Question-13, Probability density curve of 3s orbital
- Answer,
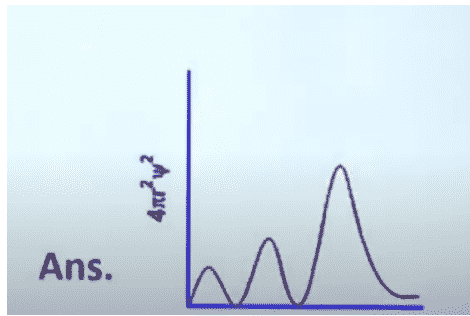
- Question,
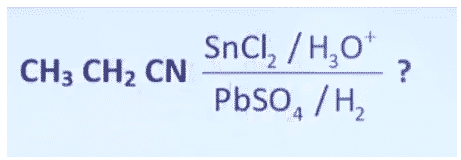
CH3CH2CH2OH - Question-14, Statement 1: CeO2 is used for the oxidation of aldehyde and ketone.
Statement 2: Aqueous solution of EuSO4 acts as a strong reducing
Both statements are true - Question-15, x/m ∝ kpx find the value of x
x = 1/n - Question-16, Ksp of AgCN is 1.2 x 10-16 find the solubility of AgCN.
√ksp - Question-17, Glycosidic linkage on lactose at which no. of C-atom
Galactose C1-C4 Glucose - Question-18,
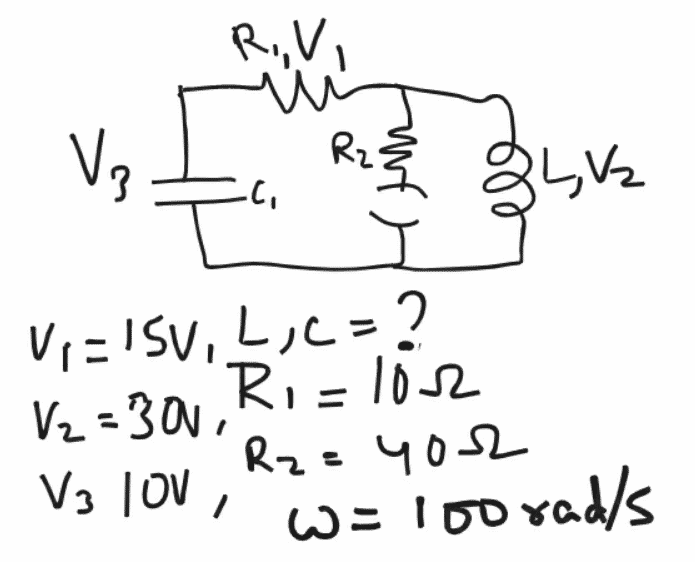
- Question-19,
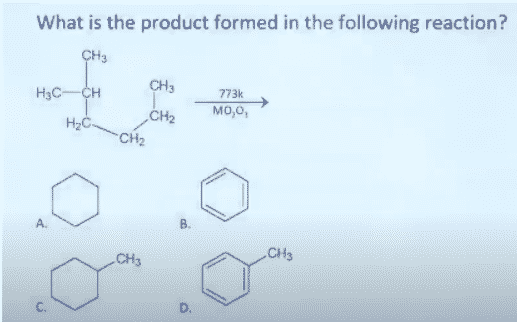
Correct Option is [D] - Question,-20 Which of the following is responsible for male secondary sexual characters?
Testoterone - Question-21, Which molecule does not exist?
Be2 - Question,
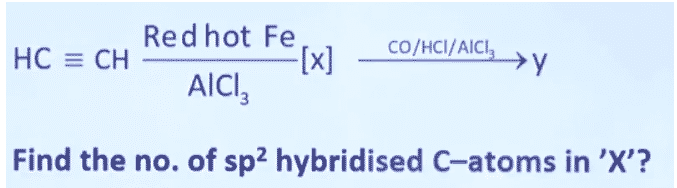
7 - Question-22, Which of the following does not hydrolysis?
SF6 - Question-23, Ellingham diagram is used for
Reduction - Question-24,
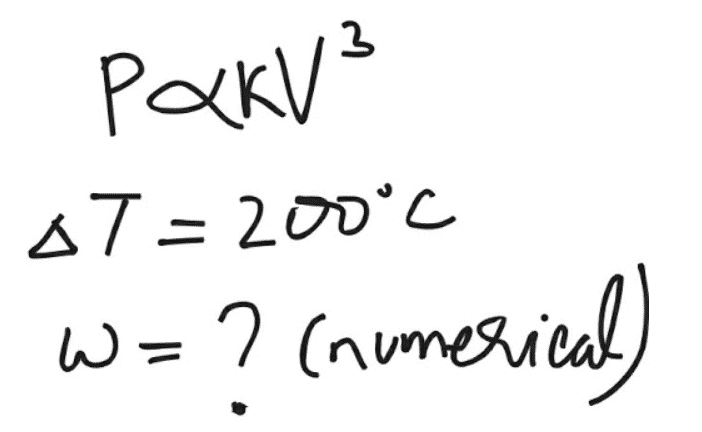
- Question-25,
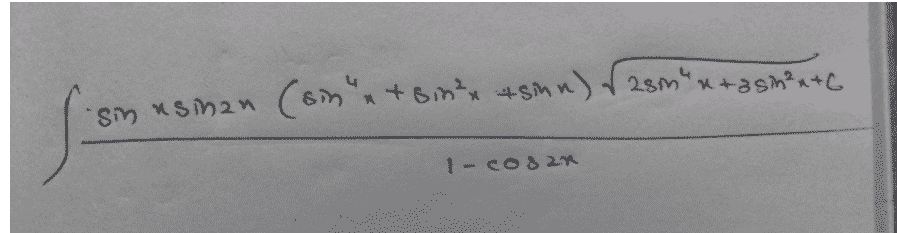
- Ques-26, Which of the following is the correct option for B2H6.
BH3 is lewis acid, Terminal H has less p character than the bridge. - Question,
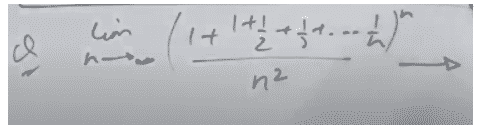
1 - Question-27,
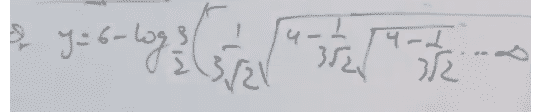
4 - Question-28,
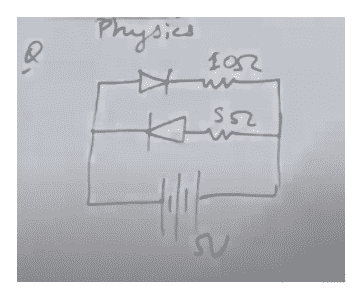
0.43 - Question-29,
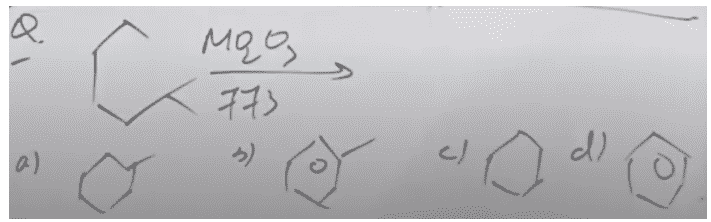
Correct option is [C] - Question,
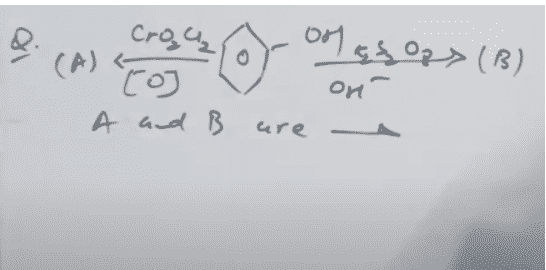
- Question-30, Which of the linkage is glucose and galactose present in lactose?
Glycosidic linkage - Question-31, Circular coil of wire consisting of 100 turns each of radius 8.0 cm carries a current of 0.40A. What is the magnitude of B at the center of the coil?
32 - Question-32, What is the focal length of the convex lens when the image size is the same when the object placed at 10 cm or 20 cm?
- Question-33, For a polytropic process whose equation is given by PVN = constant, x is not equal to 0, 1, or ⋎. Which is true?
- Question-34, A charged solid conductor having a cavity in the figure. What is the charge induced on the outer surface?
+q - Question-35, Monomer of Buna S –
1,3 – Butadiene & Syrene
The official Answer key for Session-1, February 2021- Check Here
Public Notice- Display of provisional Answer keys and Question paper with the recorded response of answer key challenge
Official JEE Main Final Answer Key
The final answer key of JEE Main February Session 2023 is released by the NTA. The answer key is given below in the form of a Pdf describing the Question ID with the Correct Option ID. The answer key is available for all Languages.
Final Answer Key 2023 for Paper-1, Session-1 
Answer Key for B.Tech/ B.E Students -2021
The answer key of February Session- 24,25, and 26 February 2021, Shift-1 and 2 is given below.
Official Answer key for Session-2, March 2021
The answer key for session -2 in 2021 is given in the following table. Candidates can check the question paper and answer key challenges by entering their application number and password or either by entering the application number and date of birth.
Display Question Paper and Answer key Challenge, March 2021- Check Here
Display of Provisional Answer Keys and Question Paper with
Recorded Responses for Answer Key Challenge – Reg.
Official Answer key for Session-3, April 2021
The answer key for session -3 (shift-1,2) released on the 5th of August 2021 is given below.
FAQs
Question-1, How I will get JEE Main Answer Key?
Candidates can get the answer key for different sets in our article or they can visit the official website. Many Coaching institutes release their answer key after the end of the exam they can also check it.
Question-2, What is the qualifying marks of JEE Main Exam?
The qualifying marks depend on the cut-off marks of the year for different categories. The NTA will release cut-off marks category wise. The expected cut-off marks are for the common rank list is 86-91, Gen EWS is 77-82, OBC – NCL is 71-76, ST is 39-44, and for SC is 51- 55.
Question-3, How we can check JEE Main previous year answer key?
Candidates can check the previous year’s answer key with the link given in the article or they can directly visit the official website to check the previous year’s answer key.
Question-4, Which type of book is considered for JEE Main Preparation?
Candidates must study the NCERT books because JEE Main Syllabus is based on the NCERT pattern and they can consider more side books like RD Sharma for Mathematics etc.
Question-5, How much time is enough for JEE Main Preparation?
Students must give 5-6 hours for self-study despite their coaching studies and solve the model paper.
Read More Articles

